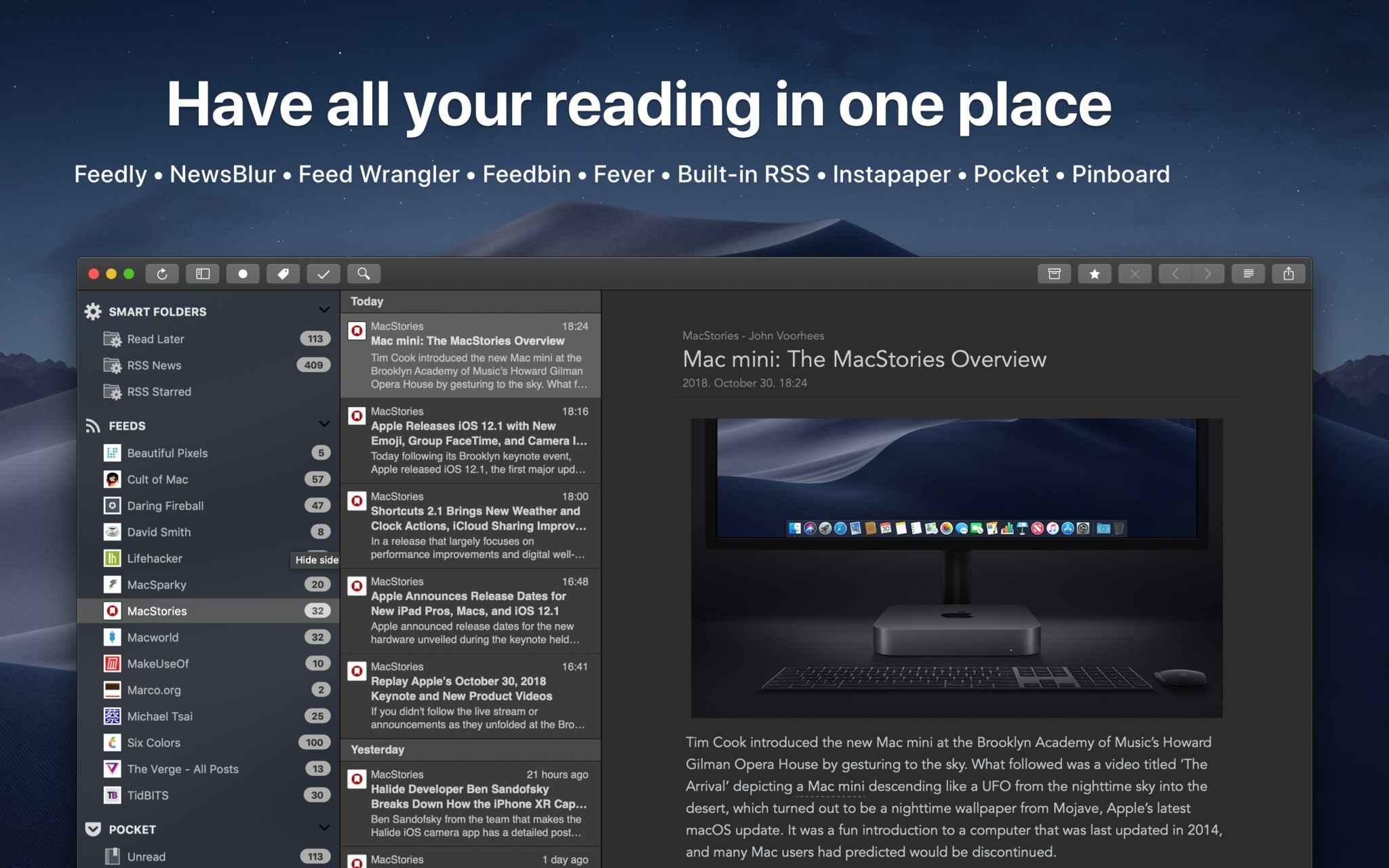
The most common simple time signatures are 2/4, 3/4, 4/4 (often indicated with a 'C' simbol) and 2/2 (often indicated with a 'cut C' simbol). In compound time signatures, each beat is divided into three equal parts. Compound time signatures are distinguished by an upper number which is commonly 6, 9 or 12. The arithmetic mean, or less precisely the average, of a list of n numbers x 1, x 2,., x n is the sum of the numbers divided by n: + + ⋯ +. The geometric mean is similar, except that it is only defined for a list of nonnegative real numbers, and uses multiplication and a root in place of addition and division: ⋅ ⋯. If x 1, x 2,., x n 0, this is equal to the. ReadKit is a full-featured read later and RSS client that supports services from Instapaper, Pocket, Pinboard, Feedly, Fever, NewsBlur, Feedbin and Feed Wrangler and has built-in RSS capabilities. MacStories: 'If you use Feed Wrangler and have been looking for a desktop client, ReadKit is yo. Many downloads like Readkit 2.6.1 Macos may also include a crack, serial number, unlock code, cd key or keygen (key generator). If this is the case it is usually found in the full download archive itself.
| Deutsche Version |
● Calculation: Amplification (gain) and damping (loss)
as factor (ratio) to the level in decibels(dB) ●
| Gain is the ratio between the magnitude of output and input signals. Gain controls on an amplifier are basically just small potentiometers (variable resistors) or volume controls, that allow you to adjust the incoming signal to the amplifier. |
The amplification factor, also called gain, is the extent to which a device boosts the strength of a signal.
The damping factor, also called loss, is the extent to which a device reduces the strength of a signal.
Enter two values and press the right calculate bar in the line of the missing answer
| The used Browser supports no Javascript. The program is indicated, but the actual function is missing. |
In analog audio engineering we deal only with 'voltage' amplification (gain) and damping (loss).
| V1 = Vin and V2 = Vout V2 > V1 or Vout > Vin means amplification. The dB value is positive (+). V2 < V1 or Vout < Vinmeans damping. The dB value is negative (−). V2/V1 or Vout/Vin means the ratio. The amplification or the damping in dB is: L = 20 × log (voltage ratio V2 / V1) in dB. V1 = Vin is the reference. |
https://zcjnd.over-blog.com/2020/12/basic-for-mac-os-x.html. In physics, attenuation is regarded as a positive value.
This naturally leads to sign errors when entering numbers.
| 3 dB ≡ | 1.414 times the voltage | (−)3 dB ≡ | damping to the value 0.707 |
| 6 dB ≡ | 2 times the voltage | (−)6 dB ≡ | damping to the value 0.5 |
| 10 dB ≡ | 3.162 times the voltage | (−)10 dB ≡ | damping to the value 0.316 |
| 12 dB ≡ | 4 times the voltage | (−)12 dB ≡ | damping to the value 0.25 |
| 20 dB ≡ | 10 times the voltage | (−)20 dB ≡ | damping to the value 0.1 |
| Using voltage we get: Level in dB: L = 20 × log (voltage ratio) |
| 6 dB = twice the voltage 12 dB = four times the voltage 20 dB = ten times the voltage 40 dB = hundred times the voltage |
If we consider audio engineering, we are usually not interested in power.
Do not ask what power amplification means.
Leave that to the telephone companies or the transmitting aerials (antennas).
Power gain is really not used in audio engineering.
Do we really need power (energy) amplification?
Read the text at the bottom.
| 3 dB ≡ | 2 times the power | (−3) dB ≡ | damping to the value 0.5 |
| 6 dB ≡ | 4 times the power | (−6) dB ≡ | damping to the value 0.25 |
| 10 dB ≡ | 10 times the power | (−10) dB ≡ | damping to the value 0.1 |
| 12 dB ≡ | 16 times the power | (−12) dB ≡ | damping to the value 0.0625 |
| 20 dB ≡ | 100 times the power | (−20) dB ≡ | damping to the value 0.01 |
Using power we get: Level in dB: L = 10 × log (power ratio) https://placanober1973.mystrikingly.com/blog/download-red-giant-trapcode-suite-14-for-mac-free.
| 3 dB = twice the power 6 dB = four times the power 10 dB = ten times the power 20 dB = hundred times the power |
If you search for the amplification ratio, given the dB value,
then go to the program dB calculation Adobe photo processing software.
Amplification (Gain) and Damping (Loss)
| To use the calculator, simply enter a value. The calculator works in both directions of the ↔ sign. |
In audio technique the following 'power or energy amplification ' is rather unusual.
| Voltage/Pressure amplification ratio | 1 | 1.414 = √2 | 2 | 3.16 = √10 | 4 | 10 | 20 | 40 | 100 | 1000 |
| Increasing of x dB | 0 | 3 | 6 | 10 | 12 | 20 | 26 | 32 | 40 | 60 |
| Power/Intensity amplification ratio | 1 | 1.414 = √2 | 2 | 3.16 = √10 | 4 | 10 | 20 | 40 | 100 | 1000 |
| Increasing of y dB | 0 | 1.5 | 3 | 5 | 6 | 10 | 13 | 16 | 20 | 30 |
|
|
| To use the calculator, simply enter a value. The calculator works in both directions of the ↔ sign. |
The voltage is always given as RMS value - but that is not valid for electric power.
There is also the reference power P0 = 1 milliwatt or 0.001 watt ≡ 0 dBm
Level in psycho acoustics as subjectivly perceived loudness (volume)The vague human feeling of the double loudness (volume) is specified
with about 6 to 10 dB. This personal feeling is not an exactly measurable value.
| Conversion Factor, Ratio, or Gain to a Level Value (Decibels dB) Amplifier conversion – Convert decibels to voltage gain / loss Calculator Voltage Gain – Voltage Loss and Power Gain – Power Loss |
Conversion: Gain G, Voltage ratioAV, and Power ratioAP
Voltage gain in dB |
Power gain in dB |
| Voltage ratio = amplification factor (voltage) |
| Power ratio = amplification factor (power) |
| V1 = Vin and V2 = Vout. V2 > V1 or Vout > Vin means amplification. The dB value is positive. (+) V2 < V1 or Vout < Vin means damping. The dB value is negative. (−) V2/V1 or Vout/Vin means the ratio. The amplification or the damping in dB is: L = 20 × log (voltage ratio V2 / V1) in dB. V1 = Vin is the reference. |
|
| back | Search Engine | home |
Here is how we specify a row vector in Octave:
Note that
- the vector is enclosed in square brackets;
- each entry is separated by an optional comma.
x = [1 3 2]results in the same row vector.
Readkit 2 6 3 Equals 1/3
To specify a column vector, we simply replace the commas with semicolons:
From this you can see that we use a comma to go to the next column of a vector (or matrix) and a semicolon to go to the next row. So, to specify a matrix, type in the rows (separating each entry with a comma) and use a semicolon to go to the next row.
You can use the standard operators to
- add (
+), - subtract (
-), and - multiply (
*)
Readkit 2 6 3 Equals 2/3
matrices, vectors and scalars with one another. Note that the matrices need to have matching dimensions (inner dimensions in the case of multiplication) for these operators to work.
- The transpose operator is the single quote:
'. To continue from the example in the previous section,
(Note: this is actually the complex conjugate transpose operator, but for real matrices this is the same as the transpose. To compute the transpose of a complex matrix, use the dot transpose (.') operator.)
- The power operator (
^) can also be used to compute real powers of square matrices.
Element operations[edit]
When you have two matrices of the same size, you can perform element by element operations on them. For example, the following divides each element of A by the corresponding element in B:
Note that you use the dot divide (./) operator to perform element by element division. There are similar operators for multiplication (.*) and exponentiation (.^).
Photo editor 2 3. Let's introduce a scalar for future use.
The dot divide operators can also be used together with scalars in the following manner.
returns a matrix, C where each entry is defined by
Cij=aBij{displaystyle C_{ij}={frac {a}{B_{ij}}}}i.e. a is divided by each entry in B. Similarly
return a matrix with
Cij=aBij{displaystyle C_{ij}=a^{B_{ij}}}You can work with parts of matrices and vectors by indexing into them. You use a vector of integers to tell Octave which elements of a vector or matrix to use. For example, we create a vector
Now, to see the second element of x, type
You can also view a list of elements as follows.
This last command displays the 1st, 3rd and 4th elements of the vector x.
To select rows and columns from a matrix, we use the same principle. Let's define a matrix
and select the 1st and 3rd rows and 2nd and 3rd columns:
The colon operator (:) can be used to select all rows or columns from a matrix. So, to select all the elements from the 2nd row, type
You can also use : like this to select all Matrix elements:
Ranges[edit]
We can also select a range of rows or columns from a matrix. We specify a range with
You can actually type ranges at the Octave prompt to see what the results are. Orange tree samples evolution strawberry (electric. For example,
The first number displayed was start, the second was start + step, the third, start + (2 * step). And the last number was less than or equal to stop.
Often, you simply want the step size to be 1. In this case, you can leave out the step parameter and type
As you can see, the result of a range command is simply a vector of integers. We can now use this to index into a vector or matrix. To select the 2×2{displaystyle 2times 2} submatrix at the top left of A, use
Finally, there is a keyword called end that can be used when indexing into a matrix or vector. It refers to the last element in the row or column. For example, to see the last column in a Matrix, you can use
The following functions can be used to create and manipulate matrices.
Creating matrices[edit]
tril(A)returns the lower triangular part of A.
triu(A)returns the upper triangular part of A.
eye(n)returns the n×n{displaystyle ntimes n} identity matrix. You can also useeye(m, n)to return m×n{displaystyle mtimes n} rectangular identity matrices.
ones(m, n)returns an m×n{displaystyle mtimes n} matrix filled with 1s. Similarly,ones(n)returns n×n{displaystyle ntimes n} square matrix.
zeros(m, n)returns an m×n{displaystyle mtimes n} matrix filled with 0s. Similarly,zeros(n)returns n×n{displaystyle ntimes n} square matrix.
rand(m, n)returns an m×n{displaystyle mtimes n} matrix filled with random elements drawn uniformly from [0,1]{displaystyle [0,1]}. Similarly,rand(n)returns n×n{displaystyle ntimes n} square matrix.
randn(m, n)returns an m×n{displaystyle mtimes n} matrix filled with normally distributed random elements.
randperm(n)returns a row vector containing a random permutation of the numbers 1,2,…,n{displaystyle 1,2,ldots ,n}.
diag(x)ordiag(A). For a vector, x, this returns a square matrix with the elements of x on the diagonal and 0s everywhere else. For a matrix, A, this returns a vector containing the diagonal elements of A. For example,
linspace(a, b, n)returns a vector with n values, such that the first element equals a, the last element equals b and the difference between consecutive elements is constant. The last argument, n, is optional with default value 100.
logspace(a, b, n)returns a vector with n values, such that the first element equals 10a{displaystyle 10^{a}}, the last element equals 10b{displaystyle 10^{b}} and the ratio between consecutive elements is constant. The last argument, n is optional with default value 50.
Other matrices[edit]
There are some more functions for creating special matrices. These are
hankel(Hankel matrix),hilb(Hilbert matrix),invhilb(Inverse of a Hilbert matrix),sylvester_matrix(Sylvester matrix) - In v3.8.1 there is a warning: sylvester_matrix is obsolete and will be removed from a future version of Octave; please use hadamard(2^k) instead,toeplitz(Toeplitz matrix),vander(Vandermonde matrix).
Use help to find out more about how to use these functions.
Changing matrices[edit]
fliplr(A)returns a copy of matrix A with the order of the columns reversed, for example,
flipud(A)returns a copy of matrix A with the order of the rows reversed, for example,
rot90(A, n)returns a copy of matrix A that has been rotated by (90n)° counterclockwise. The second argument, n{displaystyle n}, is optional with default value 1, and it may be negative.
reshape(A, m, n)creates an m×n{displaystyle mtimes n} matrix with elements taken from A. The number of elements in A has to be equal to mn{displaystyle mn}. The elements are taken from A in column major order, meaning that values in the first column (A11,…,Am1{displaystyle A_{11},ldots ,A_{m1}}) are read first, then the second column (A12,…,Am2{displaystyle A_{12},ldots ,A_{m2}}), etc.
sort(x)returns a copy of the vector x with the elements sorted in increasing order.
For a description of more operators and functions that can be used to manipulate vectors and matrices, find eigenvalues, etc., see the Linear algebra section.
Return to the Octave Programming Tutorial index
